Before you take a scored quiz for this lesson, try this set of practice questions. Your score on this self-check will be similar to to that of your scored quiz. If you do not score well on this self-check, please review this lesson and try again.
Find the inverse of f(x) = -3x.
- ƒ-1(x) = -3x
- ƒ-1(x) = -\(\small\mathsf{ \frac{1}{3} }\) x
- ƒ-1(x) = 3x -1
- ƒ-1(x) = 3x
Interchange x and y: x = -3y. Solve for y= -\(\small\mathsf{ \frac{1}{3} }\) x.
Interchange x and y: x = -3y. Solve for y= -\(\small\mathsf{ \frac{1}{3} }\) x.
Interchange x and y: x = -3y. Solve for y= -\(\small\mathsf{ \frac{1}{3} }\) x.
Interchange x and y: x = -3y. Solve for y= -\(\small\mathsf{ \frac{1}{3} }\) x.
How would you write the inverse of the set {(2,5), (0,4), (2,-3)}?
- {(-2,5), (0,4), (-2,-3)}
- {(2,-3), (0,4), (2,5)}
- {(-2,-5), (0,-4), (-2,3)}
- {(5,2), (4,0), (-3,2)}
The inverse of a set interchanges the domain and range values.
The inverse of a set interchanges the domain and range values.
The inverse of a set interchanges the domain and range values.
The inverse of a set interchanges the domain and range values.
Find the inverse of f(x) = 8x2 – 15.
- ƒ-1 (x) = \(\mathsf{\sqrt{\frac{x − 15}{8}}}\)
- ƒ-1 (x) = \(\mathsf{\sqrt{\frac{x + 15}{8}}}\)
- ƒ-1 (x) = \(\mathsf{ \frac{\sqrt{x+5}}{15 } }\)
- ƒ-1 (x) = \(\mathsf{ \frac{\sqrt{15x+8}}{15 } }\)
Interchange x and y to get: x = 8y2 -15. Next, solve for y to get: y2 = \(\mathsf{ \frac{x + 15 }{8 } }\) ; y = \(\mathsf{\sqrt{\frac{x + 15}{8}}}\).
Interchange x and y to get: x = 8y2 -15. Next, solve for y to get: y2 = \(\mathsf{ \frac{x + 15 }{8 } }\) ; y = \(\mathsf{\sqrt{\frac{x + 15}{8}}}\).
Interchange x and y to get: x = 8y2 -15. Next, solve for y to get: y2 = \(\mathsf{ \frac{x + 15 }{8 } }\) ; y = \(\mathsf{\sqrt{\frac{x + 15}{8}}}\).
Interchange x and y to get: x = 8y2 -15. Next, solve for y to get: y2 = \(\mathsf{ \frac{x + 15 }{8 } }\) ; y = \(\mathsf{\sqrt{\frac{x + 15}{8}}}\).
How does the graph of an inverse function look compared to the parent function?
- The inverse function is the parent function reflected through x-axis.
- The inverse function is the parent function reflected through y-axis.
- The inverse function is the parent function reflected through y = -x.
- The inverse function is the parent function reflected through y = x.
Inverse functions are reflections through the line y = x.
Inverse functions are reflections through the line y = x.
Inverse functions are reflections through the line y = x.
Inverse functions are reflections through the line y = x.
Summary
 Questions answered correctly:
Questions answered correctly:
 Questions answered incorrectly:
Questions answered incorrectly:
Inverse Function
The inverse of a function is produced when you interchange the domain and range of the function. The inverse is denoted with ƒ-1 (x).
For example, suppose the domain and range of a function is:
{(1, 2), (3, 5), (5, 7), (8, 10)}.
The inverse function will have the following points:
{(2, 1), (5, 3), (7, 5), (10, 8)}.
You interchange the x and y values in order to find the points of the inverse function.
Graph of an Inverse Function
The graph of an inverse function is a reflection of the original function across the line y = x. Let's look at an example.
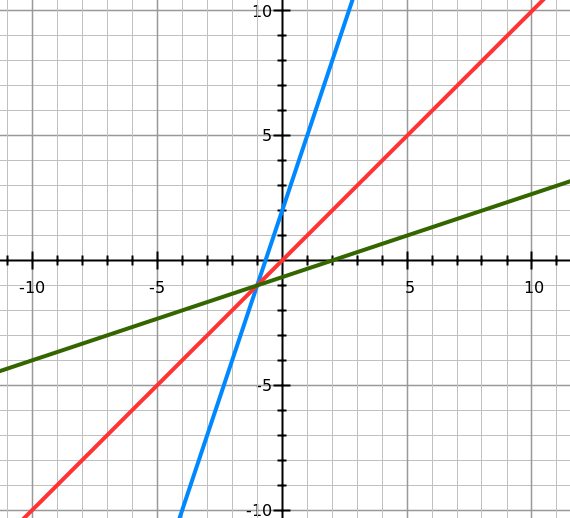
The blue graph is the original function ƒ(x) = 3x + 2.
The red graph is the function ƒ(x) = x.
The green graph is the inverse of the original function and is represented by the equation ƒ-1(x) = \(\small\mathsf{ \frac{(x-2)}{3} }\).
Think of the red line as a mirror. The original function is reflected across this mirror.
Finding the Inverse of a Linear Function
How did you find the inverse of the function ƒ(x) = 3x + 2? Remember that an inverse interchanges the domain and range of a function. The domain is all the x values while the range is all the y values. When you are given a linear function, you can interchange the x and y variables and then solve for y.
Work through the following example.
Find the inverse of ƒ(x) = 3x + 2.
Rewrite the function using y instead of ƒ(x). It will be easier to see.
y = 3x + 2
Now interchange the x and y variables and solve for y again.
| y = 3x + 2 |
| x = 3y + 2 |
| x - 2 = 3y |
| \(\small\mathsf{ \frac{(x-2)}{3} }\) = y |
The inverse function is ƒ-1(x) = \(\small\mathsf{ \frac{(x-2)}{3} }\).
Finding the Inverse of a Quadratic Function
You can also find the inverse of a quadratic function. The process is the same, but you need to be careful when dealing with square roots. Work through the following example.
Find the inverse of ƒ(x) = x2 + 2.
Rewrite the function using y instead of ƒ(x). It will be easier to see.
y = x2 + 2
Now interchange the x and y variables and solve for y again.
| y = x2 + 2 |
| x = y2 + 2 |
| x - 2 = y2 |
| y = \(\mathsf{ \pm\sqrt{x - 2 } }\) |
The number under the radical has to be positive in order for the answer to be a real number.
x − 2 ≥ 0
x ≥ 2
This means that the inverse of the function ƒ(x) = x2 + 2 is ƒ-1(x) = \(\mathsf{ \pm\sqrt{x - 2 } }\) for x ≥ 2.
Finding the Inverse of a Polynomial Function
Find the inverse of ƒ(x) = x5 − 3.
Rewrite the function using y instead of ƒ(x). It will be easier to see.
y = x5 - 3
Now, interchange the x and y variables and solve for y again.
| x = y5 - 3 |
| x + 3 = y5 |
| y = \(\mathsf{ \sqrt[5]{x + 3} }\) |
The inverse function is ƒ-1(x) = \(\mathsf{ \sqrt[5]{x + 3} }\).
Horizontal Test
You can find out whether the inverse of a function is also a function by using the horizontal line test.
Horizontal Line Test
The inverse of a function is also a function if and only if every horizontal line drawn on the function only crosses the graph at no more than one point.
Let's look at an example. The following is the graph of ƒ(x) = \(\small\mathsf{ \frac{1}{3} }\)x + 4. No matter where you draw the horizontal lines, the lines will only go through the graph at one point. This function passes the horizontal line test; therefore, the inverse of this function will also be a function.


