The concept of drawing to scale can be used to determine the similarity of two images, such as the two triangles shown below.
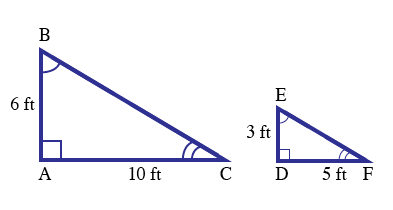
Notice that the angles in these triangles are congruent to each other, but the measurements of the corresponding sides are not equal. The two triangles are similar to each other only if the corresponding sides are proportional. (The sides don't have to be equal for the shapes to be similar.)
In algebra, you learned that to check whether the sides of two shapes are proportional, you first set up the ratios of the corresponding sides. To test these two triangles, you will need to set up ratios that compare the
side lengths.
Take another look at the diagrams. Side AB corresponds to side DE. \(\mathsf{ \triangle ABC }\) corresponds to \(\mathsf{ \triangle DEF }\). Remember that this means that ∠A should be compared to ∠D, and ∠B compared to ∠E, and ∠C compared to ∠F. The ratio of side AB to side DE can be written \(\small\mathsf{ \overline{AB}:\overline{DE} }\). Substituting in numbers, we can say 6:3, which reduces to 2:1.
Try It!
If we compare another set of sides, will we get the same ratio if these triangles are similar?
Yes. \(\small\mathsf{ \overline{AC} }\) corresponds to \(\small\mathsf{ \overline{DF} }\), so we can say \(\small\mathsf{ \overline{AC} : \overline{DF} }\). Substituting in the numbers, we get 10:5, which does simplify to 2:1.
As you can see, the ratios are equal, so we can say these two triangles are similar to each other. This can be written as \(\mathsf{ \triangle ABC \sim \triangle DEF}\).
