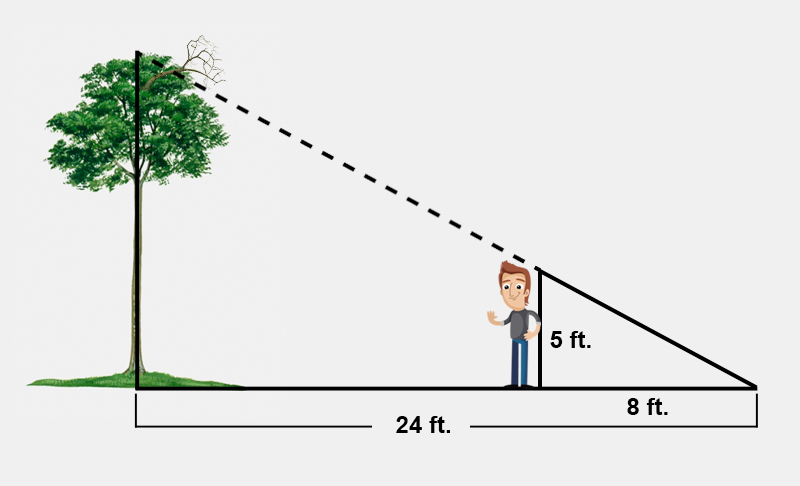
This winter was an especially harsh one for the Northeast. Storm after storm hit the states along the Atlantic coast, causing branches to break as they buckled under the weight of the ice. Eric's job is to cut down broken branches before they fall on a power line or someone's head.
As you can see in the diagram below, Eric is 5 feet tall. If he is standing 16 feet away from this tree, will a 25-foot ladder be long enough to take Eric to the top of the tree so he can remove the dangling branch? Click through the slide show below to see how Eric could answer his question and choose the right ladder for the job.
Step 1Eric might begin by labeling the given information. In this drawing, he's labeled the angles of the triangles with capital letters, and labeled the unknown height of the tree (segment AB) as "x." 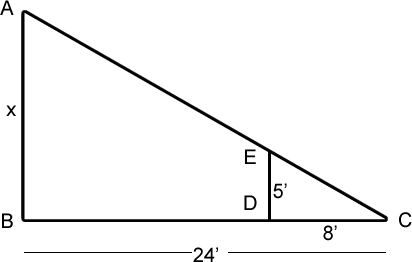
Step 2Next, to see things more clearly, Eric draws the triangles as two separate shapes. 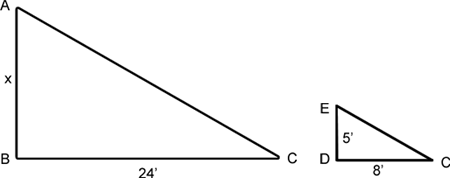
Step 3Eric sees that the corresponding angles are congruent, so he knows that the two triangles are similar. Therefore, he can use proportions to identify the length of the missing side. \(\mathsf{ \frac{5}{x} }\) = \(\mathsf{ \frac{8}{24} }\) Step 4The height of the tree, Eric learns, is 15 feet, so a 25 foot ladder is definitely big enough to solve this problem! 
|
