Geometric similarity is a key concept that you will see and use often in this course. Each of the problems below requires you to use your understanding of similarity in a slightly different way. See if you can solve all three problems using what you've learned in this lesson.

Are these two rectangles similar? How do you know? The two rectangles are similar. Their angles are the same and equal to 90°. To check whether the sides are in proportion, first set up the following ratios of the corresponding sides: \(\mathsf{ \frac{\text{shorter side of smaller rectangle}}{\text{shorter side of the larger rectangle}} = \frac{\text{longer side of shorter rectangle}}{\text{longer side of the larger rectangle}} }\) If the two are equal, the sides are in proportion. So we have \(\mathsf{ \frac{2}{3} }\) = \(\mathsf{ \frac{6}{9} }\), and they are both equal to \(\mathsf{ \frac{2}{3} }\). So we can say that the corresponding sides are 2:3 ratio. 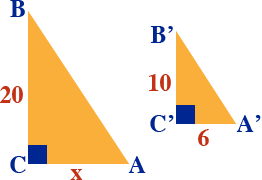
Given angle A and angle A' are each 59°, find \(\small\mathsf{ \overline{AC} }\).
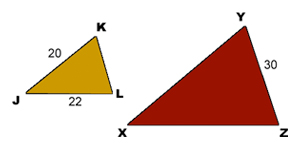
\(\mathsf{ \frac{20}{10} }\) = \(\mathsf{ \frac{x}{6} }\) If \(\small\mathsf{ \triangle{JKL} \sim \triangle{XYZ}, LJ = 22, JK = 20 \text{ and } YZ = 30 }\), what is the similarity ratio? Draw a diagram! No corresponding side lengths are given, so you cannot find the similarity ratio. There is no way to set up a ratio without at least one more known side!
|