Which statement about the figure is correct?
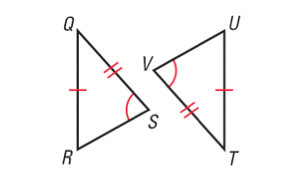
- \(\small\mathsf{ \angle{V} \cong{} \angle{S} }\)
- \(\small\mathsf{ \overline{QS} \cong{} \overline{UT} }\)
- \(\small\mathsf{ \angle{S} \cong{} \angle{T} }\)
- \(\small\mathsf{ \overline{QR} \cong{} \overline{VT} }\)
Matching number of angle and side markings denote congruence.
Matching number of angle and side markings denote congruence.
Matching number of angle and side markings denote congruence.
Matching number of angle and side markings denote congruence.
If ABCD \(\small\mathsf{ \cong{} }\)PSRQ, then which congruence statement is not true?
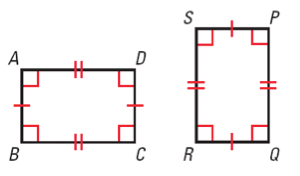
- \(\small\mathsf{ \angle{A} \cong{} \angle{Q} }\)
- \(\small\mathsf{ \overline{AB} \cong{} \overline{PQ} }\)
- \(\small\mathsf{ \overline{AD} \cong{} \overline{SR} }\)
- \(\small\mathsf{ \angle{D} \cong{} \angle{Q} }\)
Congruent figures have the corresponding sides that are congruent and corresponding angles that are congruent.
Congruent figures have the corresponding sides that are congruent and corresponding angles that are congruent.
Congruent figures have the corresponding sides that are congruent and corresponding angles that are congruent.
Congruent figures have the corresponding sides that are congruent and corresponding angles that are congruent.
Why are the figures ABCD and EFGH below similar but not congruent?
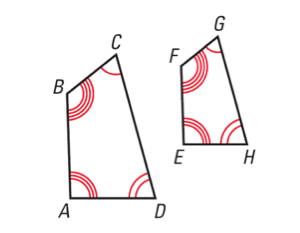
- They both have four sides.
- They both have four angles.
- They are different sizes.
- They have the same direction.
Similar figures have congruent angles, but proportional sides. In other words, they are the same shape, but not necessarily the same size.
Similar figures have congruent angles, but proportional sides. In other words, they are the same shape, but not necessarily the same size.
Similar figures have congruent angles, but proportional sides. In other words, they are the same shape, but not necessarily the same size.
Similar figures have congruent angles, but proportional sides. In other words, they are the same shape, but not necessarily the same size.
Why are these two rectangles not similar?
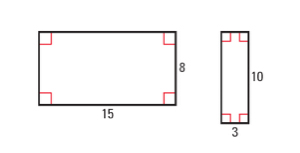
- Their sides are not proportional to one another.
- They are oriented differently on the page.
- They both have 4 angles equal to 90 degrees.
- Their sides are the same thickness.
Their sides are not proportional to one another.
Their sides are not proportional to one another.
Their sides are not proportional to one another.
Their sides are not proportional to one another.
If A ~ B, then which statement would need to be true?
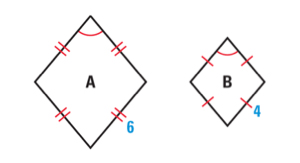
- Each pair of angles must be proportional to each other.
- The ratio of each pair of corresponding sides is \(\mathsf{ \frac{3}{2} }\).
- Each pair of corresponding sides are the same thickness.
- The figures must be able to be traced on graph paper.
Corresponding sides in similar figures have the same ratio.
Corresponding sides in similar figures have the same ratio.
Corresponding sides in similar figures have the same ratio.
Corresponding sides in similar figures have the same ratio.
Given that WXYZ ~ PQRS, what is the ratio of any pair of sides in these figures?
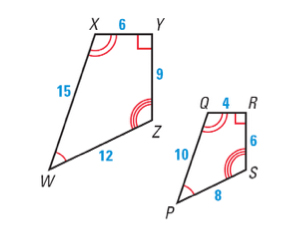
- \(\mathsf{ \frac{3}{4} }\)
- \(\mathsf{ \frac{2}{3} }\)
- \(\mathsf{ \frac{1}{2} }\)
- \(\mathsf{ \frac{3}{2} }\)
The ratio of any two sides of the figures is XY : QR = \(\mathsf{ \frac{6}{4} = \frac{3}{2} }\).
The ratio of any two sides of the figures is XY : QR = \(\mathsf{ \frac{6}{4} = \frac{3}{2} }\).
The ratio of any two sides of the figures is XY : QR = \(\mathsf{ \frac{6}{4} = \frac{3}{2} }\).
The ratio of any two sides of the figures is XY : QR = \(\mathsf{ \frac{6}{4} = \frac{3}{2} }\).
Summary
 Questions answered correctly:
Questions answered correctly:
 Questions answered incorrectly:
Questions answered incorrectly:
