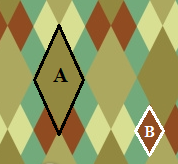
In the physical world around you, similar shapes are used by designers to create patterns, such as argyle, shown in the image to the right. (You may have seen an argyle pattern on a pair socks or a sweater.) Notice the different size diamonds, or rhombuses, that appear in the pattern. There are varying sizes with varying colors, but the shapes and their angles are identical. A \(\small\mathsf{ \sim }\) B, which reads "A is similar to B."
Because the rhombuses in an argyle pattern are similar, the corresponding angle measurements of diamond A are the same as the corresponding angle measurements of diamond B. A designer creating this pattern "from scratch" would want to measure her angles carefully to make sure the shapes will create a clear and pleasing pattern.
In the process, she might label each of the angles in the figures as shown, and note that ABCD \(\small\mathsf{ \sim }\) PQRS.
Can you name the angles that correspond with each other in the two figures?

\(\small\mathsf{ \angle{A} }\) corresponds to \(\small\mathsf{ \angle{P} }\)
\(\small\mathsf{ \angle{B} }\) corresponds to \(\small\mathsf{ \angle{Q} }\)
\(\small\mathsf{ \angle{C} }\) corresponds to \(\small\mathsf{ \angle{R} }\)
\(\small\mathsf{ \angle{D} }\) corresponds to \(\small\mathsf{ \angle{S} }\)
Since the angles correspond as shown and we know the figures are similar to each other, we know that corresponding angles are congruent. \(\small\mathsf{ \angle{A} }\) \(\small\mathsf{ \cong{} }\)\(\small\mathsf{ \angle{P} }\), \(\small\mathsf{ \angle{B} }\) \(\small\mathsf{ \cong{} }\)\(\small\mathsf{ \angle{Q} }\), \(\small\mathsf{ \angle{C} }\) \(\small\mathsf{ \cong{} }\)\(\small\mathsf{ \angle{R} }\), and \(\small\mathsf{ \angle{D} }\) \(\small\mathsf{ \cong{} }\)\(\small\mathsf{ \angle{S} }\).
Question
What is the difference between similarity and congruence?
When two shapes are similar, it means that their corresponding angles are congruent, but their sides may have different lengths. The side lengths are proportional.
