Before you move on, let's look at one last practice problem. This problem takes into consideration everything you have learned in this lesson, but its a little more difficult. If you can do this problem, you will be ready for your assessments. Answer the question below in your notes, then click the answer button to check your work.
Challenge Problem

A bike path starts on one side of the parking lot, goes around a small pond, and comes out on the other end of the parking lot. Following the path, a biker rides 100.0 meters directly east, then turns south and rides 200.0 meters. From there, she turns and rides 150.0 meters at an angle of 30.0° south of west. Turning one last time, she rides 250.0 meters at an angle of 60.0° north of west. What is her final displacement (distance and direction) from her starting point?
| P | 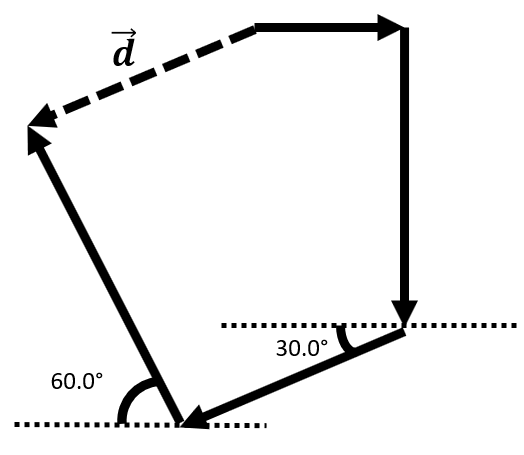 |
| I | \(\small\mathsf{\overrightarrow{d}_1 = 100.0 \text{ m}}\) at 0° \(\small\mathsf{\overrightarrow{d}_2 = 200.0 \text{ m}}\) at 270° \(\small\mathsf{\overrightarrow{d}_3 = 150.0 \text{ m}}\) 210° \(\small\mathsf{\overrightarrow{d}_4 = 250.0 \text{ m}}\) at 120° |
| R | \(\mathsf{ \sin{\theta} = \frac{opposite}{hypotenuse}}\) \(\mathsf{ \cos{\theta} = \frac{adjacent}{hypotenuse}}\) \(\small\mathsf{\tan{\theta} = \frac{opposite}{adjacent}}\) \(\small\mathsf{ c^2 = a^2 + b^2 }\) |
| A | \(\small\mathsf{\overrightarrow{d}_{x_1} = (100.0 \text{ m}) (\cos0) = 100.0 \text{ m} }\) \(\small\mathsf{\overrightarrow{d}_{y_1} = (100.0 \text{ m}) (\sin0) = -0.0 \text{ m} }\) \(\small\mathsf{\overrightarrow{d}_{x_2} = (200.0 \text{ m}) (\cos270) = 0.0 \text{ m} }\) \(\small\mathsf{\overrightarrow{d}_{y_2} = (200.0 \text{ m}) (\sin270) = -200.0 \text{ m} }\) \(\small\mathsf{\overrightarrow{d}_{x_3} = (150.0 \text{ m}) (\cos210) = -129.9 \text{ m} }\) \(\small\mathsf{\overrightarrow{d}_{y_3} = (150.0 \text{ m}) (\sin210) = -75.0 \text{ m} }\) \(\small\mathsf{\overrightarrow{d}_{x_4} = (250.0 \text{ m}) (\cos120) = -125.0 \text{ m} }\) \(\small\mathsf{\overrightarrow{d}_{y_5} = (250.0 \text{ m}) (\sin120) = 216.5 \text{ m} }\) \(\small\mathsf{\overrightarrow{d}_{x} = \overrightarrow{d}_{x_1} + \overrightarrow{d}_{x_2} = \overrightarrow{d}_{x_3} + \overrightarrow{d}_{x_4}}\) \(\small\mathsf{\overrightarrow{d}_{x} = 100.0 \text{ m} + 0.0 \text{ m} + -129.9 \text{ m} + -125.0 \text{ m} = -154.9 \text{ m}}\) \(\small\mathsf{\overrightarrow{d}_{y} = \overrightarrow{d}_{y_1} + \overrightarrow{d}_{y_2} + \overrightarrow{d}_{y_3} + \overrightarrow{d}_{y_4} }\) \(\small\mathsf{\overrightarrow{d}_{y} = 0.0 \text{ m} + -200.0 \text{ m} + -75.0 \text{ m} + 216.5 \text{ m} = -58.5 \text{ m} }\) \(\small\mathsf{ c^2 = (-154.9 \text{ m})^2 + (-58.5 \text{ m})^2 }\) \(\small\mathsf{ c = \sqrt{27416.26 \text{ m}^2} = 165.6 \text{ m}}\) \(\small\mathsf{\theta = tan^{-1}(\frac{-58.5 \text{ m}}{-154.9 \text{ m}}) = 20.69° }\) |
| T | \(\small\mathsf{ \overrightarrow{d} = 165.6 \text{ m}}\) \(\small\mathsf{\theta = 20.7° }\) |
| E | The biker is 165.6 meters away from her starting point at an angle of 20.7° south of west. |
