Andrei wants to climb the side of the Great Pyramid of Giza. He knows that the base is 230 meters and that it is 140 meters tall. Using the Pythagorean Theorem and the tangent function, he knows he has enough information to find how far he will have to climb and at what angle. Try the calculation in your notes and then click answer button below to check your work.
| P | 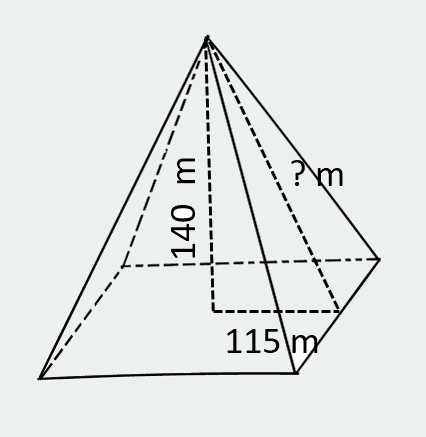 |
| I | adjacent = 115 meters opposite = 140. meters |
| R | \(\small\mathsf{ c^2 = a^2 + b^2 }\) \(\small\mathsf{\tan{\theta} = \frac{opposite}{adjacent}}\) |
| A | \(\small\mathsf{ c^2 = (115. \text{ meters})^2 + (140. \text{ meters})^2 }\) \(\small\mathsf{ c^2 = 13225 \text{ meters}^2 + 19600 \text{ meters}^2 }\) \(\small\mathsf{ c = \sqrt{32825 \text{ meters}^2} = 181.18 \text{ meters}}\) \(\small\mathsf{\tan{\theta} = \frac{140. \text{ meters}}{115. \text{ meters}}}\) \(\small\mathsf{tan^{-1}\tan{\theta} = tan^{-1}(1.217) }\) \(\small\mathsf{\theta = 50.599° }\) |
| T | \(\small\mathsf{ \text{resultant magnitude} = 181 \text{ meters}}\) \(\small\mathsf{\theta = 50.6° }\) |
| E | He will have to walk a total of 181 meters at an angle of 50.6° N of E. |
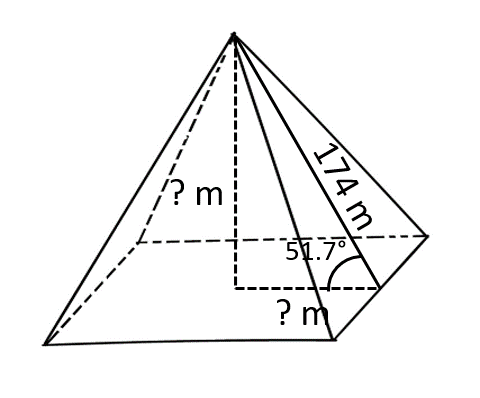
After he conquered the Great Pyramid of Giza, he went on to visit the neighboring Pyramid of Khafre. He knows that he will have to hike a total distance of 174 meters at an angle of 51.7° north of east to get to the top of that one. How can he find the width and height of the pyramid? He will have to find the two components of the displacement to find this information.
Question
In this case, we are given what we used to call the resultant vector instead of two perpendicular vectors. If we want to find the two equivalent vectors that would add up to this resultant vector, what trigonometric functions can we use?
We are given the hypotenuse of the right triangle this time, so we can use the sine and cosine functions to find the vertical and horizontal component vectors.