Don't Assume
Don't Assume
Just because the example problems have used cosine for the x-direction and sine for the y-direction, don't assume that will always be the case. The correct function will be determined by which component is adjacent and which is opposite of the angle you have in your drawing.
| SOH | CAH |
|---|---|
| \(\mathsf{ \sin{\theta} = \frac{opposite}{hypotenuse}}\) | \(\mathsf{ \cos{\theta} = \frac{adjacent}{hypotenuse}}\) |
Find the component vectors in each of the examples below. Click on each cell in the table to check your work.
| Problem | Picture | Given/Find | Equation | Solution |
|---|---|---|---|---|
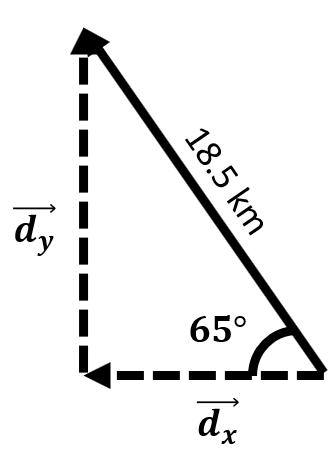
| A hiker walks 18.5 kilometers at an angle of 65° north of west from base camp. What are the horizontal and vertical components of her displacement? |
|
\(\small\mathsf{\overrightarrow{d} = 18.5 \text{ km}}\) at 115° | \(\small\mathsf{\sin{\theta} = \frac{opposite}{hypotenuse} }\) \(\small\mathsf{ \cos{\theta} = \frac{adjacent}{hypotenuse}}\) |
\(\small\mathsf{\overrightarrow{d}_x = (18.5 \text{ km})(\cos115) = -7.8 \text{ km} }\) \(\small\mathsf{\overrightarrow{d}_y = (18.5 \text{ km})(\sin115) = 16.8 \text{ km} }\) |
| A truck is going up a 14.5° incline with a speed of 26.8 m/s. What is the horizontal and vertical components of the truck's velocity? |
|
\(\small\mathsf{\overrightarrow{v} = 26.8 \text{ m/s}}\) at 14.5° | \(\small\mathsf{\sin{\theta} = \frac{opposite}{hypotenuse} }\) \(\small\mathsf{ \cos{\theta} = \frac{adjacent}{hypotenuse}}\) |
\(\small\mathsf{\overrightarrow{v}_x = (26.8 \text{ m/s})(\cos14.5) = 25.9 \text{ m/s} }\) \(\small\mathsf{\overrightarrow{v}_y = (26.8 \text{ m/s})(\sin14.5) = 6.71 \text{ m/s} }\) |
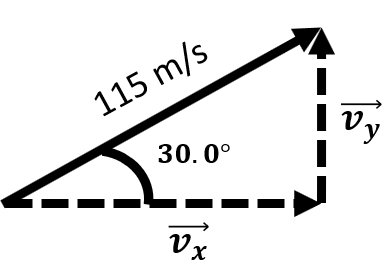
| A plane takes off from the ground at an angle of 30.0° with the horizontal at a speed of 115 m/s. What is the horizontal and vertical components of the airplane's velocity? |
|
\(\small\mathsf{\overrightarrow{d} = 115 \text{ m/s}}\) at 30.0° | \(\small\mathsf{\sin{\theta} = \frac{opposite}{hypotenuse} }\) \(\small\mathsf{ \cos{\theta} = \frac{adjacent}{hypotenuse}}\) |
\(\small\mathsf{\overrightarrow{v}_x = (115 \text{ m/s})(\cos30.0) = 99.6 \text{ m/s} }\) \(\small\mathsf{\overrightarrow{v}_y = (115 \text{ m/s})(\sin30.0) = 57.5 \text{ m/s} }\) |
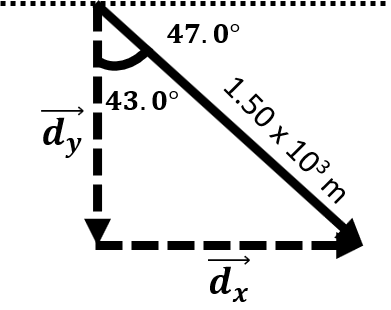
| Standing at the precipice of a mountain, a hiker sees the bottom of the mountain through a spyglass at 1.50 x 103 feet away at an angle of depression of 47° south of east. What is the hiker's horizontal and vertical displacement from the bottom of the mountain? |
|
\(\small\mathsf{\overrightarrow{d} = 1.50 \times 10^3 \text{ m}}\) at 313° | \(\small\mathsf{\sin{\theta} = \frac{opposite}{hypotenuse} }\) \(\small\mathsf{ \cos{\theta} = \frac{adjacent}{hypotenuse}}\) |
\(\small\mathsf{\overrightarrow{d}_x = (1.50 \times 10^3 \text{ m}) (\cos313) = 1.02 \times 10^3 \text{ m} }\) \(\small\mathsf{\overrightarrow{d}_y = (1.5 \times 10^3 \text{ m}) (\sin313) = -1.10 \times 10^3 \text{ m} }\) |
Question
Did you notice that the problems all used the angle measures from 0° to 360°. Why is it done that way?
Using the actual unit circle angles provides the answers is positive and negatives, so you will always get an accurate direction on the components. It is okay to ignore those and use the angles given in the problems, as long as you always revisit your picture to determine the signs of the components. If you choose to use angles in the coordinate plane 0-360°, then, the x-component will always use the cosine function and the y-components will always use the sine function.