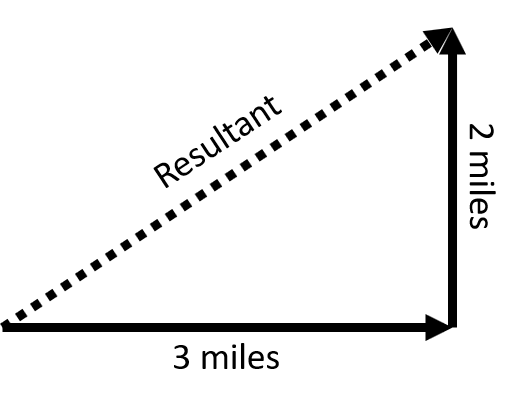
Up until this point, you have seen vector additional problems with vectors in one dimension and two dimensions. The two-dimensional problems have all had perpendicular vectors. You now know how to add vectors that are pointing in the same or opposite direction, as well as adding vectors that are perpendicular. Click on each image below to review those processes.
Let's expand our understanding of adding vectors to adding two-dimensional vectors that are not perpendicular to one another. In this, you will actually apply the concepts you just learned about finding component vectors of a vector at an angle. Click through the slide show to see the thought process behind adding non-perpendicular vectors.
|
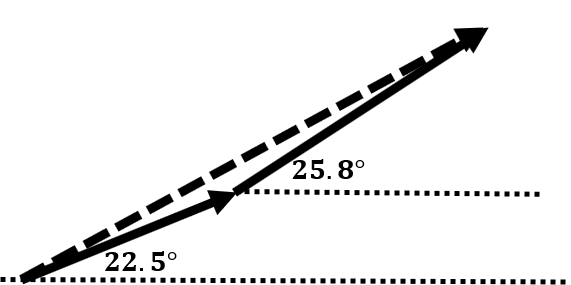
Consider the example problem: An airplane first ascends at 22.5° to the ground for 15.0 km and then increases its angle of ascent to 25.8° to the ground for an additional 28.5 km. How can we determine the magnitude and direction of the plane's total displacement? Let's set a frame of reference and think about the problem graphically. If we drew the two vectors tip to tail, the resultant would be a large vector that connects the first vector's tip to the second vector's tail.
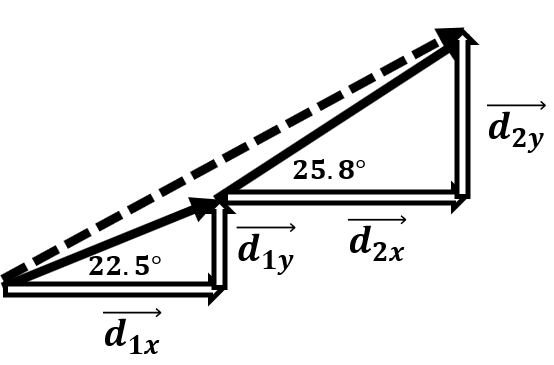
To find the resultant vector looks difficult, but it can be simplified by finding the horizontal and vertical components of each vector and then adding the perpendicular vectors.
Find the x and y components of each vector using the method you are familiar with.
\(\small\mathsf{\overrightarrow{d}_{x_1} = 15.0 \text{ km} (\cos22.5) = 13.9 \text{ km} }\) \(\small\mathsf{\overrightarrow{d}_{x_2} = 28.5 \text{ km} (\cos25.8) = 25.7 \text{ km} }\) Now, we are left with a familiar adding perpendicular vectors problem. First, we need to find the sums in the horizontal and vertical directions.
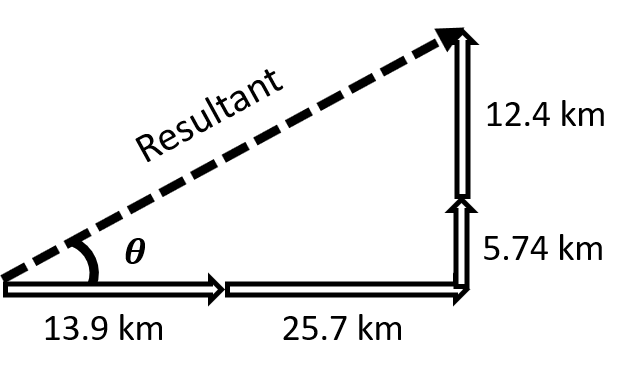
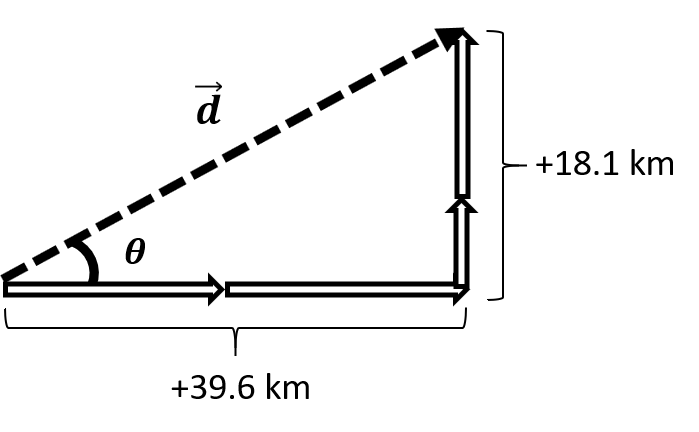
\(\small\mathsf{\overrightarrow{d}_{x} = \overrightarrow{d}_{x_1} + \overrightarrow{d}_{x_2} = +13.9 \text{ km} + +25.7 \text{ km} = +39.6 \text{ km}}\) \(\small\mathsf{\overrightarrow{d}_{y} = \overrightarrow{d}_{y_1} + \overrightarrow{d}_{y_2} = +5.74 \text{ km} + +12.4 \text{ km} = +18.1 \text{ km} }\) Next, we can use the Pythagorean Theorem and the tangent function to find the resultant displacement of the airplane.
\(\small\mathsf{ c^2 = (39.6 \text{ km})^2 + (18.1 \text{ km})^2 }\) \(\small\mathsf{\tan{\theta} = \frac{18.1 \text{ km}}{39.6 \text{ km}}}\) The airplane's final displacement is 43.5 kilometers at 24.6° north of east from its starting point. |