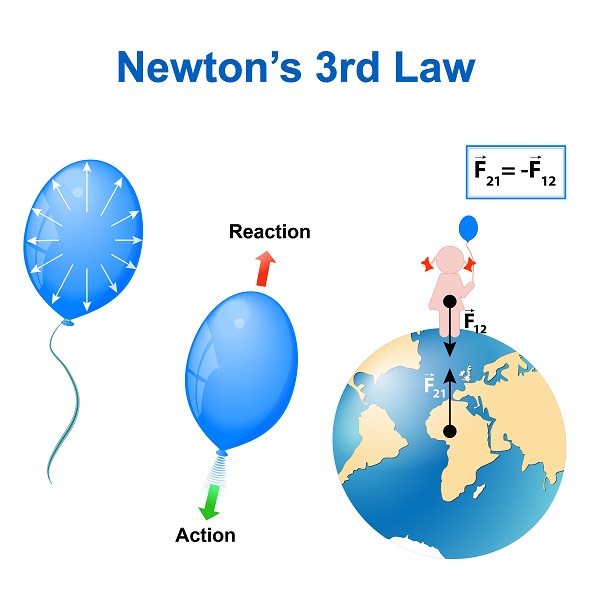
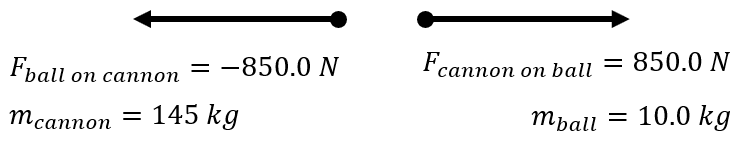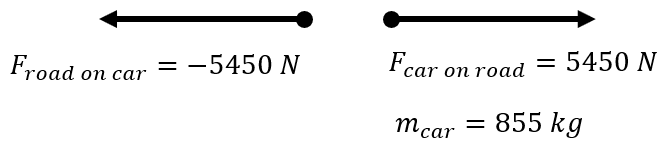Newton's Third Law equates the force that an object A exerts on object B is equal and opposite to the force that B exerts on A at that same instant. You can use this knowledge to solve force problems, but you must treat the two objects separately, since the forces act on two different objects.
Complete the following practice problems using the concepts from both Newton's Second Law and Newton's Third Law. Once you have tried the problems on your own, click the answer button to check your work.
| Problem | Picture | Given/Find | Equation | Solution |
|---|---|---|---|---|
| A 10.0 kg cannonball is fired from a 145 kg cannon with a force of 850.0 N to the East. What is the force acting on the cannon? What is the acceleration of the cannonball? What is the acceleration of the cannon? |
\(\small\mathsf{
\overrightarrow{F}_{\text{ball on cannon}}
= -850.0 \text{ N} }\) \(\small\mathsf{ m_{cannon} = 145 \text{ kg} }\) \(\small\mathsf{\overrightarrow{a}_{cannon} = ? \text{ m/s}^2 }\) \(\small\mathsf{ \overrightarrow{F}_{\text{cannon on ball}} = 850.0 \text{ N} }\) \(\small\mathsf{ m_{ball} = 10.0 \text{ kg} }\) \(\small\mathsf{\overrightarrow{a}_{ball} = ? \text{ m/s}^2 }\) |
\(\small\mathsf{
\overrightarrow{F}_{\text{ball on cannon}}
= m_{cannon} \overrightarrow{a}_{cannon}
}\) \(\small\mathsf{ \overrightarrow{F}_{\text{cannon on ball}} = m_{ball} \overrightarrow{a}_{ball} }\) |
\(\small\mathsf{ -850.0 \text{ N} = (145
\text{ kg}) \overrightarrow{a}_{cannon}
}\) \(\small\mathsf{\overrightarrow{a}_{cannon} = \frac{-850.0 \text{ N}}{145 \text{ kg}} }\) \(\small\mathsf{\overrightarrow{a}_{cannon} = 5.86 \text{ m/s}^2 }\) \(\small\mathsf{ 850.0 \text{ N} = (10.0 \text{ kg}) \overrightarrow{a}_{ball} }\) \(\small\mathsf{\overrightarrow{a}_{ball} = \frac{850.0 \text{ N}}{10.0 \text{ kg}} }\) \(\small\mathsf{\overrightarrow{a}_{ball} = 85.0 \text{ m/s}^2 }\) |
|
| An 855 kg car pushes on the road with +5450 N. What is the magnitude of the force acting on the car? What is the acceleration of the car? |
\(\small\mathsf{
\overrightarrow{F}_{\text{car on road}} =
+5450 \text{ N} }\) \(\small\mathsf{ \overrightarrow{F}_{\text{road on car}} = ? \text{ N} }\) \(\small\mathsf{ m_{car} = 855 \text{ kg} }\) \(\small\mathsf{\overrightarrow{a}_{road} = ? \text{ m/s}^2 }\) |
\(\small\mathsf{
\overrightarrow{F}_{\text{car on road}} =
-\overrightarrow{F}_{\text{road on car}}
}\) \(\small\mathsf{ \overrightarrow{F}_{\text{road on car}} = m_{car} \overrightarrow{a}_{car} }\) |
\(\small\mathsf{ +5450 \text{ N} =
-\overrightarrow{F}_{\text{road on car}}
}\) \(\small\mathsf{ \overrightarrow{F}_{\text{road on car}} = -5450 \text{ N} }\) \(\small\mathsf{ -5450 \text{ N} = (855 \text{ kg}) \overrightarrow{a}_{car} }\) \(\small\mathsf{\overrightarrow{a}_{car} = \frac{-5450 \text{ N}}{855 \text{ kg}} }\) \(\small\mathsf{\overrightarrow{a}_{car} = 6.37 \text{ m/s}^2 }\) |
|
| A baseball player hits a baseball with his bat causing the 0.145 kg ball to accelerate at 24.0 m/s2. What was the force on the ball? What was the force on the bat? What is the acceleration of the bat given its mass is 0.935 kg? |
\(\small\mathsf{
\overrightarrow{F}_{\text{bat on ball}} =
? \text{ N} }\) \(\small\mathsf{ m_{ball} = 0.145 \text{ kg} }\) \(\small\mathsf{\overrightarrow{a}_{ball} = 24.0 \text{ m/s}^2 }\) \(\small\mathsf{ \overrightarrow{F}_{\text{ball on bat}} = ? \text{ N} }\) \(\small\mathsf{ m_{bat} = 0.935 \text{ kg} }\) \(\small\mathsf{\overrightarrow{a}_{bat} = ? \text{ m/s}^2 }\) |
\(\small\mathsf{
\overrightarrow{F}_{\text{bat on ball}} =
m_{ball} \overrightarrow{a}_{ball} }\) \(\small\mathsf{ \overrightarrow{F}_{\text{bat on ball}} = -\overrightarrow{F}_{\text{ball on bat}} }\) \(\small\mathsf{ \overrightarrow{F}_{\text{ball on bat}} = m_{bat} \overrightarrow{a}_{bat} }\) |
\(\small\mathsf{
\overrightarrow{F}_{\text{bat on ball}} =
(0.145 \text{ kg})(24.0 \text{ m/s}^2)
}\) \(\small\mathsf{ \overrightarrow{F}_{\text{bat on ball}} = 3.48 \text{ N} }\) \(\small\mathsf{ 3.48 \text{ N} = -\overrightarrow{F}_{\text{ball on bat}} }\) \(\small\mathsf{ \overrightarrow{F}_{\text{ball on bat}} = -3.48 \text{ N} }\) \(\small\mathsf{ -3.48 \text{ N} = (0.935 \text{ kg}) \overrightarrow{a}_{bat} }\) \(\small\mathsf{\overrightarrow{a}_{bat} = \frac{-3.48 \text{ N}}{0.935 \text{ kg}} }\) \(\small\mathsf{\overrightarrow{a}_{bat} = -3.72 \text{ m/s}^2 }\) |