Another Example

Let's look at the example 9030 ÷ 34. This one had so many steps that it didn’t really make sense to use the powers of 10. It helped us to understand how using powers of 10 works, but grouping the powers will work better.

	First, we can see that 34 x 200 = 6800:
	Now, 2230 is a fairly large number, and we already know that we used several groups of ten 34s when we solved the problem before. But, if we didn't know how many groups of ten 34s to use, how would we decide? To decide how many 34s to use, look at the first digits of 2230 (22) and the first digit of 34; 3 (the first digit in 34) goes into 22 seven times, so we could try 34 x 70 first. 34 x 70 = 2,380. This is more than we need, so we should try 34 x 60; 34 x 60 = 2,040. That will work: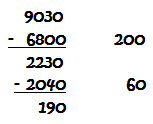
	Now that there's only 190 left, think about how many times 30 (close to 34) goes into 190; 6 x 30 = 180. That's pretty close, so let's try 6 x 34. This equals 204, so it's too much. Try 34 x 5. This is equal to 170, so we should use 5: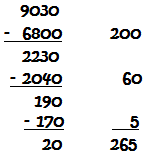

This is much shorter than using just the powers of 10!